Model-free reinforcement learning (RL) can be used to learn effective policies for complex tasks, such as Atari games, even from image observations. However, this typically requires very large amounts of interaction – substantially more, in fact, than a human would need to learn the same games. How can people learn so quickly? Part of the answer may be that people can learn how the game works and predict which actions will lead to desirable outcomes. In this paper, we explore how video prediction models can similarly enable agents to solve Atari games with fewer interactions than model-free methods. We describe Simulated Policy Learning (SimPLe), a complete model-based deep RL algorithm based on video prediction models, and present a comparison of several model architectures, including a novel architecture that yields the best results in our setting.
URL: arxiv.org/abs/1903.00374
Topic: Model-Based RL
Video: www.youtube.com/watch?v=fblsbJL2ycU
1. Background
How is it that humans can learn these games so much faster? Perhaps part of the puzzle is that humans possess an intuitive understanding of the physical processes that are represented in the game: we know that planes can fly, balls can roll, and bullets can destroy aliens. We can therefore predict the outcomes of our actions. In this paper, we explore how learned video models can enable learning in the Atari Learning Environment (ALE) benchmark. Although prior works have proposed training predictive models for next-frame, future-frame, as well as combined future-frame and reward predictions in Atari games, no prior work has successfully demonstrated model-based control via predictive models that achieve competitive results with model-free RL.
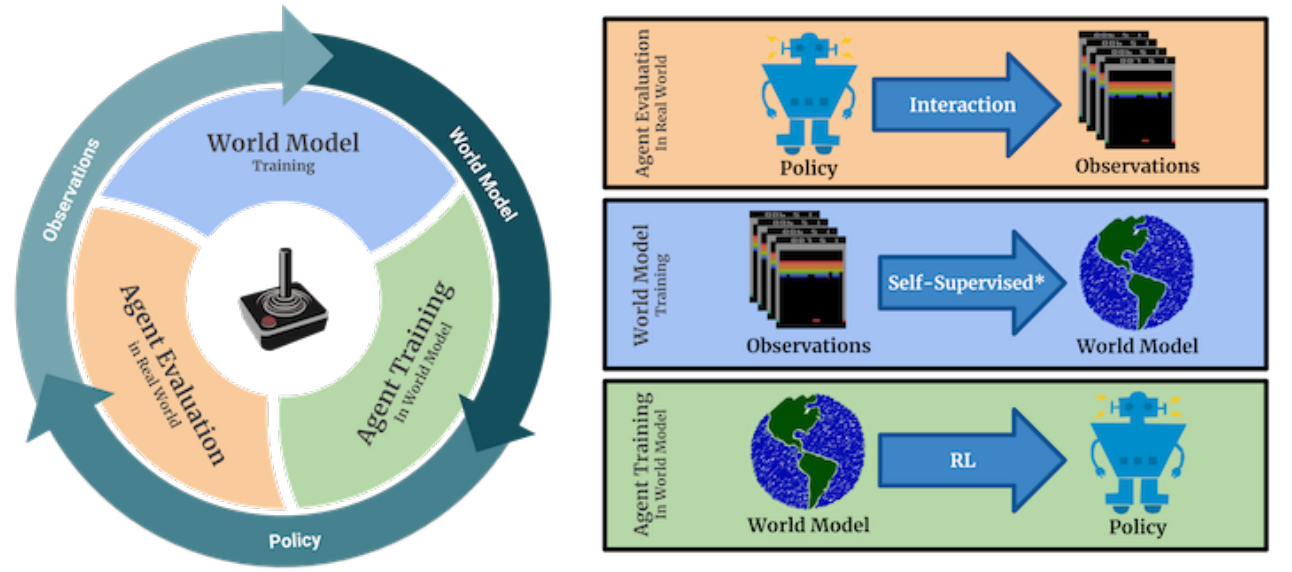
Using models of environments, or informally giving the agent ability to predict its future, has a fundamental appeal for reinforcement learning. The spectrum of possible applications is vast, including learning policies from the model, capturing important details of the scene, encouraging exploration, creating intrinsic motivation or counterfactual reasoning. One of the exciting benefits of model-based learning is the promise to substantially improve the sample efficiency of deep reinforcement learning. Our work advances the state-of-the-art model-based reinforcement learning by introducing a system that, to our knowledge, is the first to successfully handle a variety of challenging games in the ALE benchmark. To that end, we experiment with several stochastic video prediction techniques, including a novel model based on discrete latent variables. We present an approach, called Simulated Policy Learning (SimPLe), that utilizes these video prediction techniques and trains a policy to play the game within the learned model. In our empirical evaluation, we find that SimPLe is significantly more sample-efficient than a highly tuned version of the state-of-the-art Rainbow algorithm (Hessel et al., 2018) on almost all games. The structure of the model-based RL algorithm that we employ consists of alternating between learning a model, and then using this model to optimize a policy with model-free reinforcement learning.
2. Simulated Policy Learning
In this work, we refer to MDPs as environments and assume that environments do not provide direct access to the state (i.e., the RAM of the Atari 2600 emulator). Instead, we use visual observations, typically $210 \times 160$ RGB images. A single image does not determine the state. In order to reduce the environment's partial observability, we stack four consecutive frames and use them as the observation. Policy $\pi$ is a mapping from states to probability distributions over $\mathcal{A}$. The quality of a policy is measured by the value function $\mathbb{E}_{\pi}\left(\sum_{t=0}^{+\infty} \gamma^{t} r_{t+1} \mid s_{0}=s\right)$, which for a starting state $s$ estimates the total discounted reward gathered by the agent.
Apart from an Atari 2600 emulator environment $env$ we will use a neural network simulated environment $env'$ which we call a world model. The environment $env'$ shares the action space and reward space with $env$ and produces visual observations in the same format, as it will be trained to mimic $env$. Our principal aim is to train a policy π using a simulated environment $env'$ so that π achieves good performance in the original environment $env$. In this training process, we aim to use as few interactions with $env$ as possible. The initial data to train $env'$ comes from random rollouts of $env$. As this is unlikely to capture all aspects of $env$, we use the iterative method presented in Algorithm 1.

2.1. World Models
In search of an effective world model, we propose a novel stochastic video prediction model (Figure 2) which achieved superior results compared to other previously proposed models. In this section, we describe the details of this architecture and the rationale behind our design decisions.
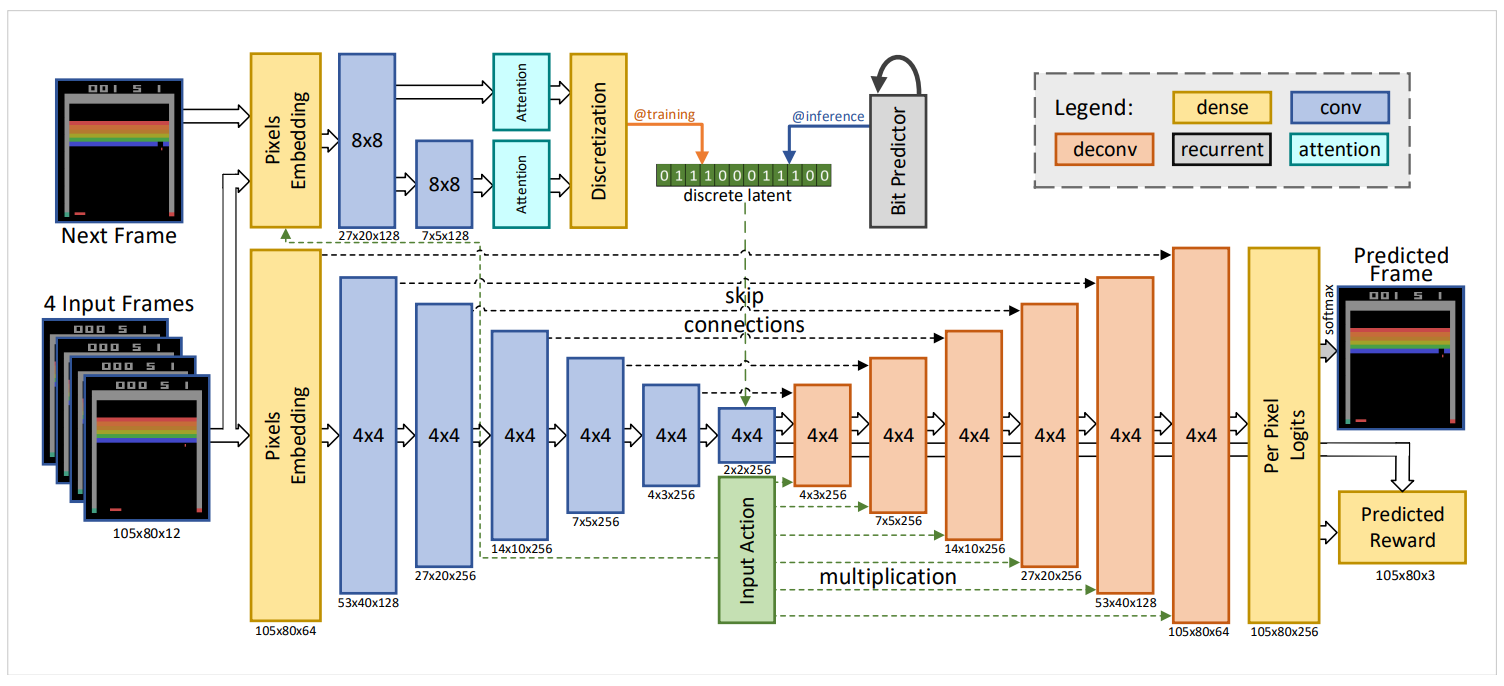
The input to the model is four stacked frames (as well as the action selected by the agent) while the output is the next predicted frame and expected reward. Input pixels and action are embedded using fully connected layers, and there is a per-pixel softmax (256 colors) in the output. The actions are one-hot-encoded and embedded in a vector which is multiplied channel-wise with the output of the convolutional layers. The network outputs the next frame of the game and the value of the reward.
This model has two main components. First, the bottom part of the network (deterministic) consists of a skip-connected convolutional encoder and decoder. To condition the output on the actions of the agent, the output of each layer in the decoder is multiplied with the (learned) embedded action. Note that a stochastic model is also used to deal with a limited horizon of past observed frames. Inspired by Babaeizadeh et al. (2017a), we tried a variational autoencoder to model the stochasticity of the environment. The second part of the model (stochastic) is a convolutional inference network that approximates the posterior given the next frame, similarly to Babaeizadeh et al. (2017a). At training time, the sampled latent values from the approximated posterior will be discretized into bits. To keep the model differentiable, the backpropagation bypasses the discretization following Kaiser & Bengio (2018). A third LSTM based network is trained to approximate each bit given the previous ones. At inference time, the latent bits are predicted auto-regressively using this network. The deterministic model has the same architecture as this figure but without the inference network.
2.2. Policy Training
We will now describe the details of SimPLe, outlined in Algorithm $1.$ In step 6 we use the proximal policy optimization (PPO) algorithm (Schulman et al., 2017) with $\gamma=0.95.$ The algorithm generates rollouts in the simulated environment $e n v^{\prime}$ and uses them to improve policy $\pi.$ The fundamental difficulty lays in imperfections of the model compounding over time. To mitigate this problem we use short rollouts of $e n v^{\prime}$. Typically every $N=50$ step we uniformly sample the starting state from the ground-truth buffer $D$ and restart $e n v^{\prime}. Using short rollouts may have a degrading effect as the PPO algorithm does not have a way to infer effects longer than the rollout length. To ease this problem, in the last step of a rollout we add to the reward the evaluation of the value function. Training with multiple iterations re-starting from trajectories gathered in the real environment is new to our knowledge.
The main loop in Algorithm 1 is iterated 15 times (cf. Section 6.4). The world model is trained for 45K steps in the first iteration and for 15K steps in each of the following ones. Shorter training in later iterations does not degrade the performance because the world model after the first iteration captures already part of the game dynamics and only needs to be extended to novel situations. In each of the iterations, the agent is trained inside the latest world model using PPO. In every PPO epoch, we used 16 parallel agents collecting 25,50 or 100 steps from the simulated environment $e n v^{\prime}$ (see Section $6.4$ for ablations).



